什么是背包问题

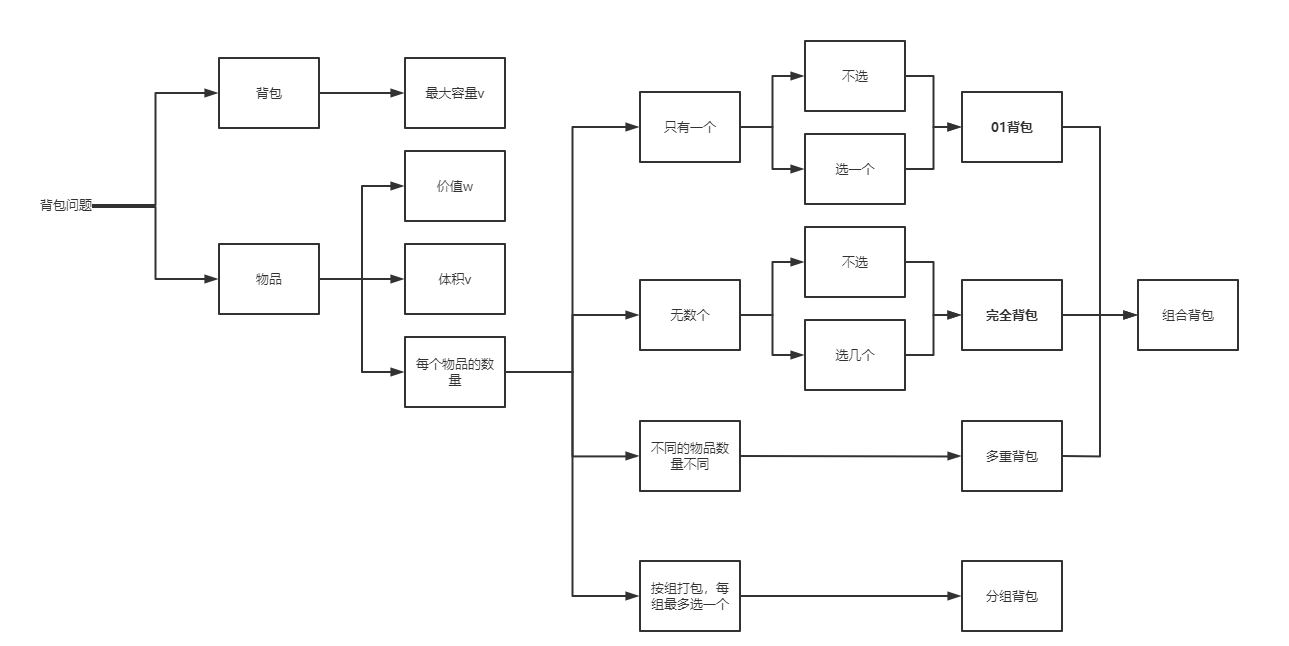
01背包（重点）

有N件物品和一个最多能被重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

以上就是一个经典的01背包问题。

二维dp数组01背包

假设背包最大重量为4，物品为：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

问背包能背的物品最大价值是多少？

1. dp[i, j]表示从下表i为0-i的物品中任意取，放进容量为j的背包，价值总和最大是多少

2. dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])

3. dp[i][0] = 0, dp[0][j] = 15

4. 确定遍历顺序，先遍历物品再遍历背包重量（均可，但先遍历物品更好理解）

   // weight数组的大小 就是物品个数
   for(int i = 1; i < weight.size(); i++) { // 遍历物品
       for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
           if (j < weight[i]) dp[i][j] = dp[i - 1][j]; 
           else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
   
       }
   }

5. 推导一遍dp数组

   | | 0 | 1 | 2 | 3 | 4 |
   |:—-:|:—-:|:—-:|:—-:|:—-:|:—-:|
   | 物品0 | 0 | 15 | 15 | 15 | 15 |
   | 物品1 | 0 | 15 | 15 | 20 | 35 |
   | 物品2 | 0 | 15 | 15 | 20 | 35 |

难点：初始化和遍历顺序

一维dp数组（滚动数组）

原递推公式为：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i] + value[i]])，dp[i][j]的值只与上一层的值有关，所以可以只用一个一维数组

1. dp[j] 表示容量为j的背包，所背的物品价值可以最大为dp[j]

2. dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

3. 初始为0

4. 遍历顺序

   for(int i = 0; i < weight.size(); i++) { // 遍历物品
       for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
           dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
       }
   }

   [注意]：二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小。倒叙遍历是为了保证物品i只被放入一次！。但如果一旦正序遍历了，那么物品0就会被重复加入多次！

5. 推导一遍

   物品0：

   | 0 | 15 | 15 | 15 | 15 |
   |:—-:|:—-:|:—-:|:—-:|:—-:|

   物品1：

   | 0 | 15 | 15 | 20 | 35 |
   |:—-:|:—-:|:—-:|:—-:|:—-:|

   物品2：

   | 0 | 15 | 15 | 20 | 35 |
   |:—-:|:—-:|:—-:|:—-:|:—-:|

应用

1. leetcode-416. 分割等和子集
2. leetcode-494. 目标和
3. leetcode-474. 一和零

完全背包

有 N 件物品和一个最多能背重量为 W 的背包。第 i 件物品的重量是 weight[i] ，得到的价值是 value[i]。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。

举例：背包最大重量为4。

每件物品都有无限个，物品为：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

回顾01背包的遍历顺序，因为要保证每个物品只被添加一次，所以遍历背包容量时是倒序的。而完全背包的物品是可以添加多次的，所以可以直接正序遍历。

//先遍历物品
for(int i = 0; i < weight.size(); i++){
    //再遍历背包
    for(int j = weight[i]; j < bagWeight; j++){
        dp[j] = max(dp[j], dp[i - weight[i]] + value[i]);
    }
}

01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了，一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。

在完全背包中，对于有一维dp数组来说，其实两个for循环嵌套顺序同样无所谓

// 先遍历背包
for(int j = 0; j <= bagWeight; j++) {
    //再遍历物品
    for(int i = 0; i < weight.size(); i++) {
        if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
    cout << endl;
}

以上所描述的都是对于纯完全背包问题，其 for 循环的先后循环是可以颠倒的！

应用

1. leetcode-518. 零钱兑换II
2. leetcode-377. 组合总和IV
3. leetcode-70. 爬楼梯
4. leetcode-322. 零钱兑换
5. leetcode-279. 完全平方数
6. leetcode-139. 单词拆分

参考

1. 代码随想录