本文最后更新于:June 20, 2022 pm
预备知识
二叉查找树
二叉查找树又叫二叉排序树,也叫二叉搜索树,左节点小于根节点,右节点大于根节点。没有键值相等的结点。
示例图:
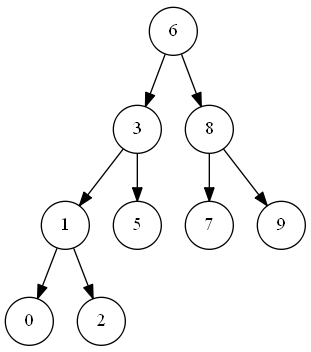
实现:
| public class BinarySearchTree<T> {
T data;
BinarySearchTree<T> left;
BinarySearchTree<T> right;
public BinarySearchTree(T data){
this(data, null, null);
}
public BinarySearchTree(T data, BinarySearchTree<T> left, BinarySearchTree<T> right) {
this.data = data;
this.left = left;
this.right = right;
}
}
|
平衡二叉树
每一个结点的左子树和右子树的高度差最多为1的二叉查找树。因此查找、插入和删除的时间复杂度都变成了O(logn)
为了反映每个结点的高度差,在二叉查找树的结点中应该增加一个新的域——被称为平衡因子(BF),它的值是某个根结点的左子树深度减右子树深度的值。易知,对于一棵平衡二叉树,每个结点的平衡因子只可能是-1、0、1三种可能
红黑树
含有红黑结点并能自平衡的二叉查找树,时间复杂度为O(logn)
一颗含有n个结点的红黑树的高度最多为2log(n+1)
性质:
- 每个结点要么是黑色,要么是红色
- 根结点是黑色
- 每个叶子结点是黑色
- 每个红色结点的两个子结点一定都是黑色,可以出现连续的黑色结点
- 任意一结点到每个叶子结点的路径都包含数量相同的黑结点
- 如果一个结点存在黑子结点,那么该结点肯定有两个子结点
下图为一颗红黑树,其中的红色结点H和M同样存在叶子结点,并且是黑色的
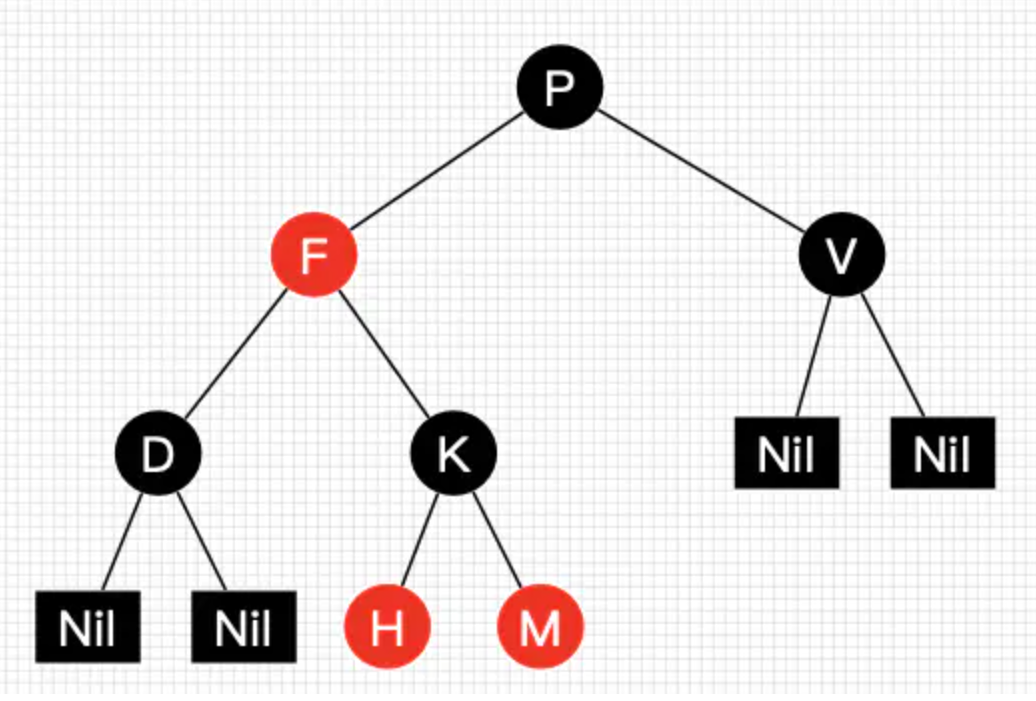
红黑树并不是一个完美平衡二叉查找树,根结点P的左子树显然比右子树高,但左子树和右子树的黑结点的层数是相等的,这种平衡叫做黑色完美平衡
红黑树实现代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| public class RBTree<T extends Comparable<T>, D>{
private RBNode<T, D> root;
private static final Boolean RED = false;
private static final Boolean BLACK = true;
public class RBNode<T extends Comparable<T>, D>{
private Boolean color;
private T key;
private D data;
private RBNode<T, D> parent;
private RBNode leftChild;
private RBNode rightChild;
public RBNode(Boolean color, T key, D data, RBNode<T, D> parent, RBNode leftChild, RBNode rightChild) {
this.color = color;
this.key = key;
this.data = data;
this.parent = parent;
this.leftChild = leftChild;
this.rightChild = rightChild;
}
}
...
}
|
红黑树能够自平衡靠的是三种操作,分别是左旋,右旋和变色
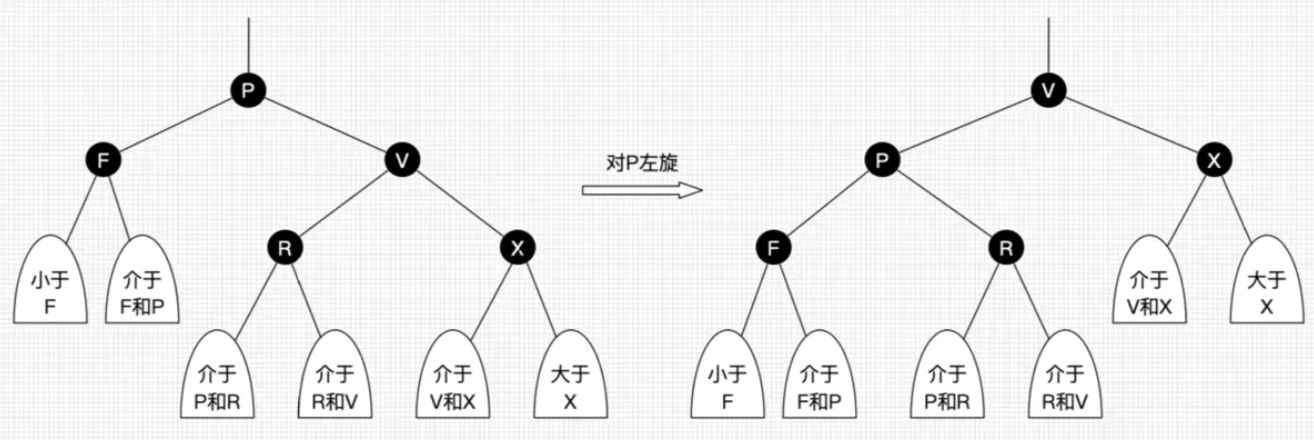
- 左旋:以某个结点为支点,其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变
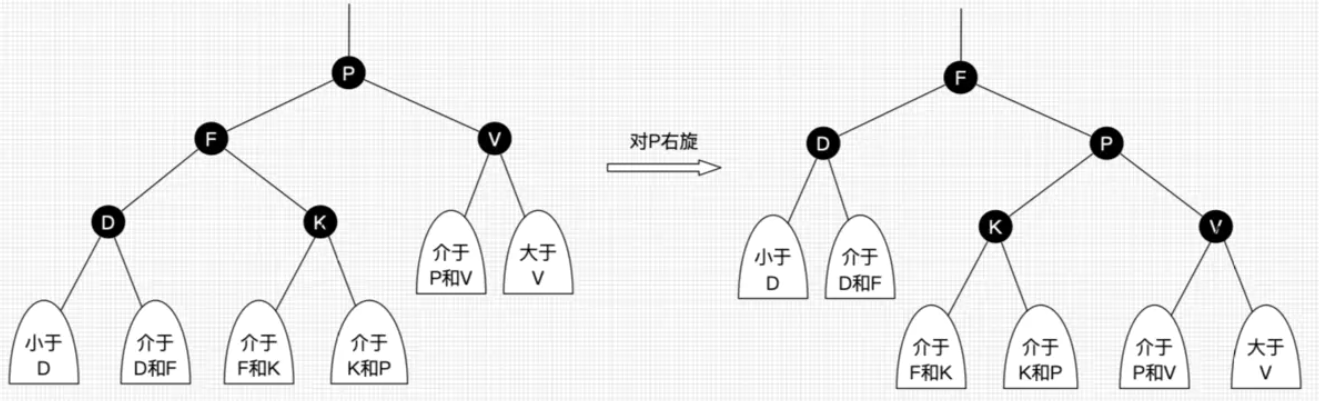
- 右旋:以某个结点为支点,其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变
- 变色:结点的颜色由红变黑或由黑变红
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
public void leftRotate(RBNode<T, D> x) {
RBNode<T, D> y = x.rightChild;
if (y.leftChild != null) {
y.leftChild.parent = x;
}
x.rightChild = y.leftChild;
y.leftChild = x;
y.parent = x.parent;
if (x.parent != null) {
if (x.parent.leftChild == x) {
x.parent.leftChild = y;
} else {
x.parent.rightChild = y;
}
} else {
this.root = y;
}
x.parent = y;
}
public void rightRotate(RBNode<T, D> x) {
RBNode<T, D> y = x.leftChild;
if (y.rightChild != null) {
y.rightChild.parent = x;
}
y.parent = x.parent;
x.leftChild = y.rightChild;
y.rightChild = x;
if (x.parent != null) {
if (x.parent.leftChild == x) {
x.parent.leftChild = y;
} else {
x.parent.rightChild = y;
}
} else {
this.root = y;
}
x.parent = y;
}
|
小结:
- 左旋只影响旋转结点和其右子树的结构,把右子树的结点往左子树移了
- 右旋只影响旋转结点和其左子树的结构,把左子树的结点往右子树移了
红黑树查找
等同于二叉查找树的查找,下图为查找的流程图
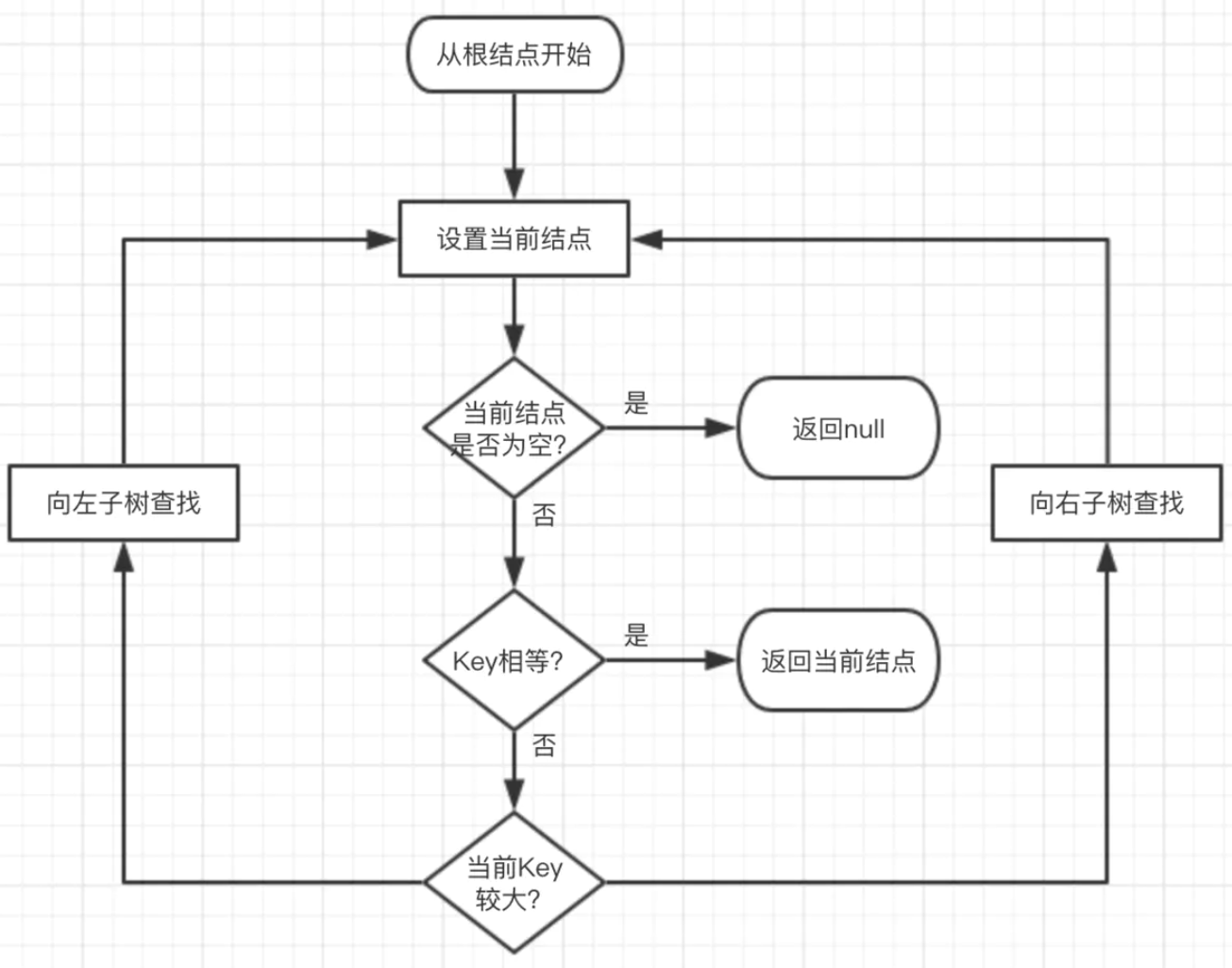
由于红黑树黑色完美平衡的特性,所以查找的最坏时间复杂度为O(2logn)
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
public RBNode<T, D> search(T key, RBNode<T, D> node) {
if (node != null) {
int com = key.compareTo(node.key);
if (com < 0) {
return search(key, node.leftChild);
} else if (com > 0) {
return search(key, node.rightChild);
} else {
return node;
}
}
return null;
}
public RBNode<T, D> iterativeSearch(T key, RBNode<T, D> node) {
if (node != null){
int com = key.compareTo(node.key);
if (com < 0){
node = node.leftChild;
} else if (com > 0){
node = node.rightChild;
} else {
return node;
}
}
return null;
}
|
红黑树插入
红黑树的插入主要分为两部分:
- 查找插入的位置即寻找插入的父结点
- 插入后自平衡
下图为查找插入位置的流程图:
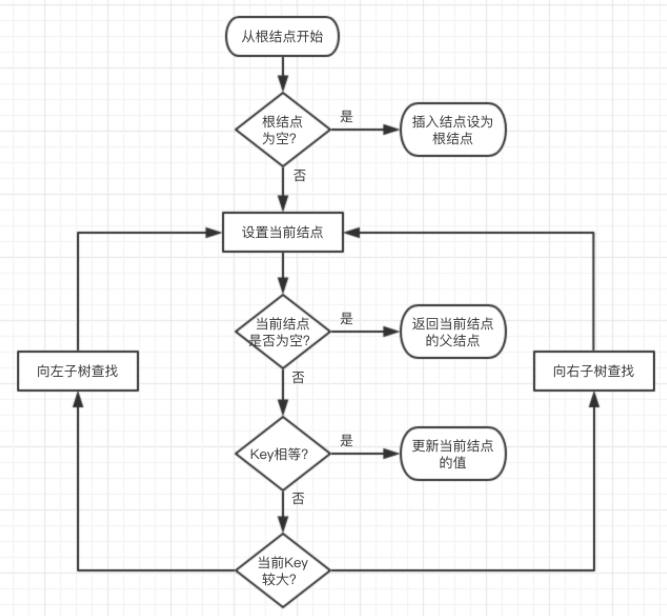
红黑树的插入场景有很多种,分别如下图所示:

注:I表示插入结点,P表示插入结点的父结点,S表示插入结点的叔叔结点,PP表示插入结点的祖父结点
插入示例:
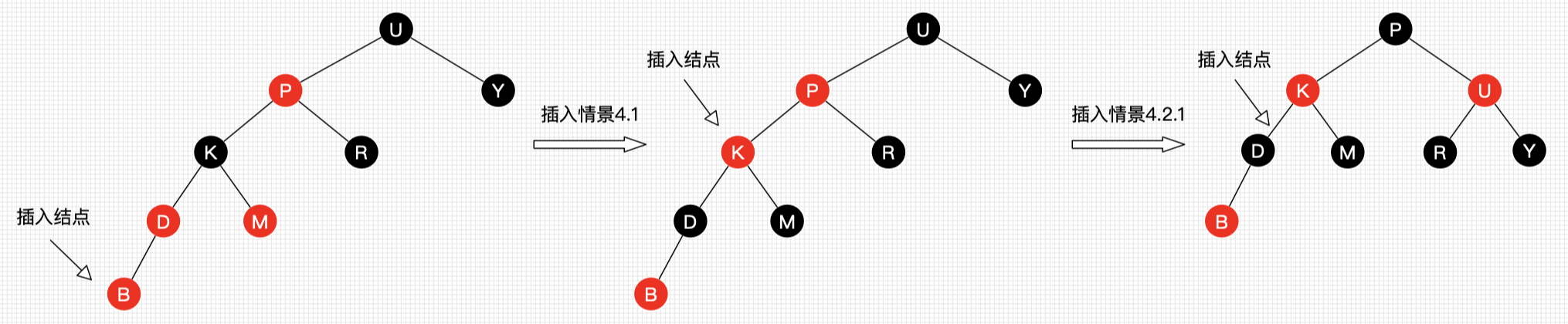
代码(略)
红黑树删除
红黑树的删除也包含两部分:
- 查找目标结点
- 删除后自平衡
二叉树删除结点找替代结点有3种情情景:
- 情景1:若删除结点无子结点,直接删除
- 情景2:若删除结点只有一个子结点,用子结点替换删除结点
- 情景3:若删除结点有两个子结点,用后继结点(大于删除结点的最小结点)替换删除结点
把二叉树所有结点投射在X轴上,所有结点都是从左到右排好序的,所有目标结点的前后结点就是对应前继和后继结点
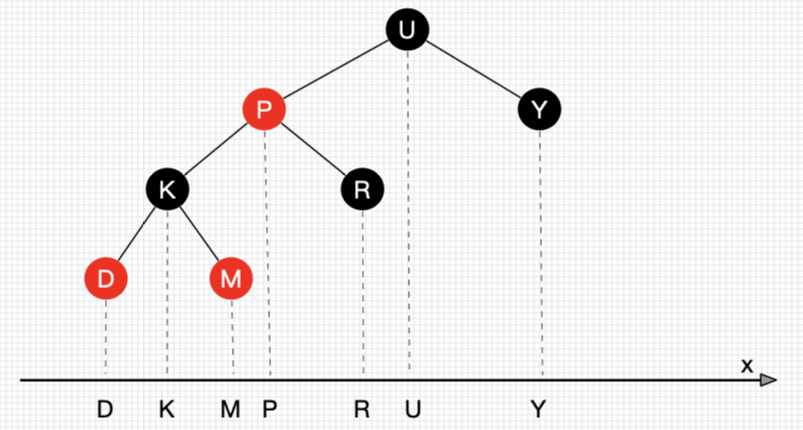
思路:删除结点被替代后,在不考虑结点的键值的情况下,对于树来说,可以认为删除的是替代结点

因此3种删除情景均可转换为情景1:
- 情景2:删除结点用其唯一的子结点替换,子结点替换为删除结点后,可以认为删除的是子结点,若子结点又有两个子结点,那么相当于转换为情景3,一直自顶向下转换,总是能转换为情景1
- 情景3:删除结点用后继结点(肯定不存在左结点),如果后继结点有右子结点,那么相当于转换为情景2,否则转为为情景1
小结:删除操作删除的结点可以看作删除替代结点,而替代结点最后总是在树末,所以只用考虑删除树末结点的情景
红黑树删除操作的所有情景如下图:
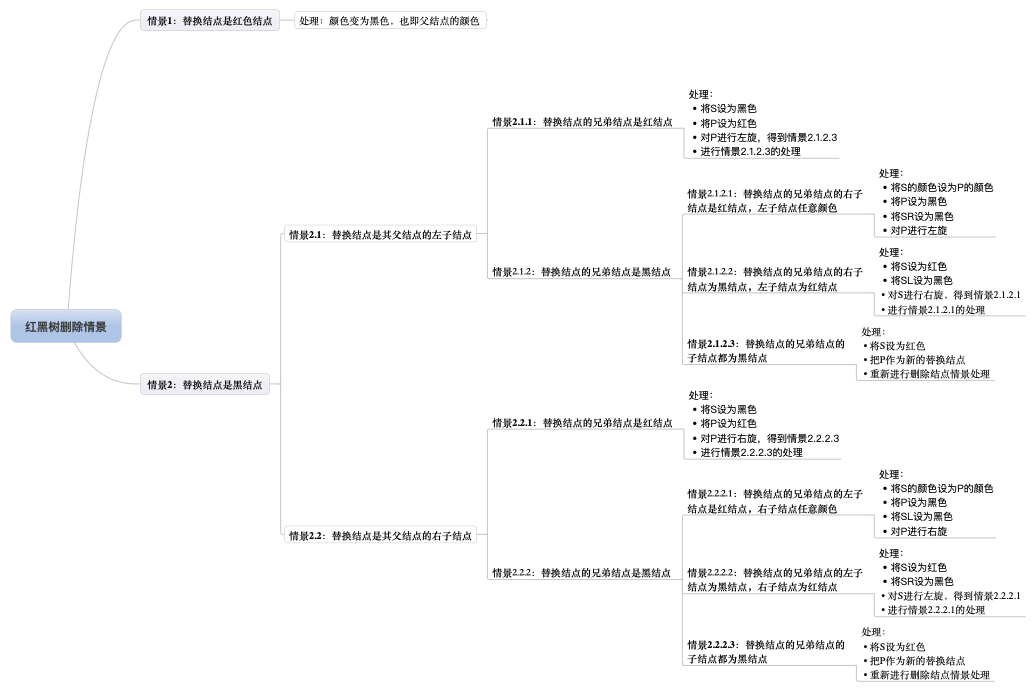
注:R表示替代结点,P表示替代结点的父结点,S表示替代结点的兄弟结点,SL表示兄弟结点的左子结点,SR表示兄弟结点的右子结点。灰色结点表示它可以是红色也可以是黑色
删除示例:
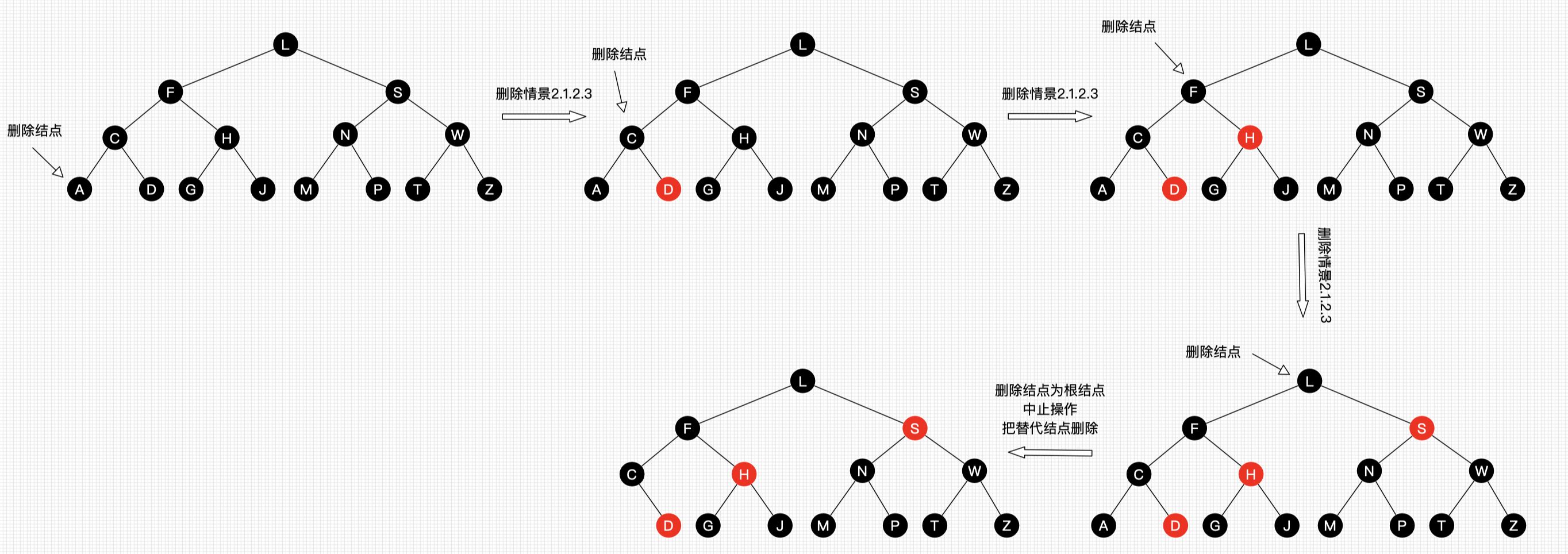
代码(略)
参考
- 数据结构(二):二叉搜索树(Binary Search Tree) - 简书
- 数据结构与算法—从平衡二叉树(AVL)到红黑树 - 简书
- 30张图带你彻底理解红黑树 - 简书











