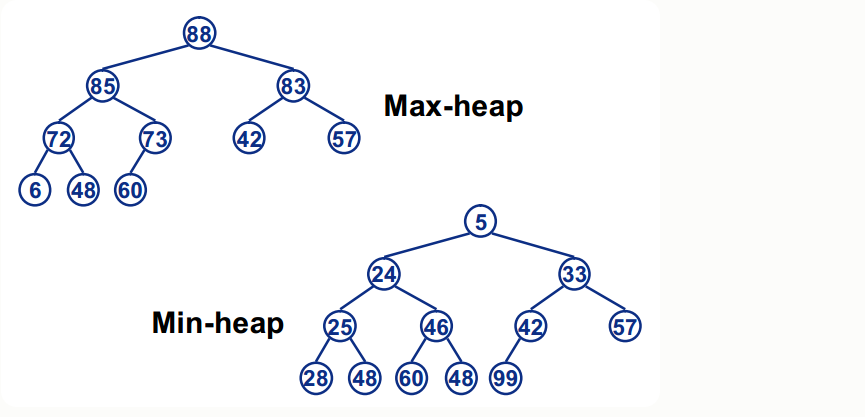
大根堆

大根堆就是根节点是整颗树的最大值（根节点大于等于左右子树的最大值），对于他的任意子树，根节点也是最大值。小根堆则相反

要求：

• 根节点的关键字既大于或等于左子树的关键字值，又大于或等于右子树的关键字值

• 为完全二叉树，所以可以用数组来存储。i结点的父结点下标就为 (i – 1) / 2

  它的左右子结点下标分别为2 * i + 1和2 * i + 2

创建大根堆

比如一棵树有 N 个元素，存放在数组里分别对应0 ~ N-1，假设数组中从0到 i - 1 位置的元素是一个大根堆，然后把第 i 个位置的元素插入大根堆里，构造一个新的大根堆，就需要从第i个位置的元素开始，依次看它的父节点是否小于它，如果小于就进行交换，直到它的父节点不小于它，或者到了该大根堆的最顶端的根节点。

/**
 * 创建大根堆
 */
public static void heapInsert(int[] arr, int index){
    //当前节点是否大于父节点
    while (arr[index] > arr[(index - 1) / 2]){
        swap(arr, index, (index - 1) / 2);
        index = (index - 1) / 2;
    }
}

/**
 * 交换两个不同位置的元素
 */
private static void swap(int[] arr, int i, int j){
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

public static void main(String[] args) {
    int[] arr = {9,43,-54,4,-13,10,36};
    for (int i = 0; i < arr.length; i++) {
        heapInsert(arr, i);
    }
    System.out.println(Arrays.toString(arr));
}

调整大根堆

设数组中对应的大根堆的长度为 heapSize 。当数组中下标为 index 的元素的值发生了变化，就要对这个堆进行调整，保证它还是大根堆。

具体过程是：将 index 对应的元素和它的左右子节点的值进行比较，如果比它小的话，就把 index 对应的元素和它的左右子节点中最大的值进行交换，交换后对他的子节点也执行这个过程。

/**
 * 调整堆
 */
public static void heapAdjust(int[] arr, int index, int heapSize){
    //左子节点
    int left = index * 2 + 1;
    //右子节点
    int right = left + 1;
    while (left < heapSize){
        //求左右子节点的最大值索引
        int max = right < heapSize && arr[right] > arr[left] ? right : left;
        //与父节点比较判断是否交换
        max = arr[max] > arr[index] ? max : index;
        if (max == index){
            break;
        }
        swap(arr, max, index);
        index = max;
        left = index * 2 + 1;
    }
}

堆排序

利用创建大根堆和调整大根堆来进行排序。

创建完大根堆以后，每一次都把堆顶的元素和堆的最后一个元素进行交换，并且把堆的长度heapSize减小1，然后对新的堆进行调整，重新调整为大根堆，然后再取堆顶的元素和堆的最后一个节点进行交换，大根堆的长度heapSize减小1，然后再调整，重复这个过程，直到堆里面剩余的元素个数为1。

/**
 * 堆排序
 */
public static void heapSort(int[] arr){
    //判断数组是否为空或是否长度为1
    if (arr == null || arr.length < 2){
        return;
    }
    //创建大根堆
    for (int i = 0; i < arr.length; i++) {
        heapInsert(arr, i);
    }
    int size = arr.length;
    //交换堆顶和堆的最后一个元素，并把堆的长度减1
    swap(arr, 0, --size);
    while (size > 0){
        //调整堆
        heapAdjust(arr, 0, size);
        //交换堆顶和堆的最后一个元素，并把堆的长度减1
        swap(arr, 0, --size);
    }
}

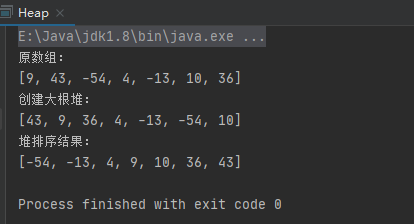
程序执行结果：

应用

leetcode剑指offer第40题

参考答案

用一个大根堆实时维护数组的前 k 小值。首先将前 k 个数插入大根堆中，随后从第 k+1 个数开始遍历，如果当前遍历到的数比大根堆的堆顶的数要小，就把堆顶的数弹出，再插入当前遍历到的数。最后将大根堆里的数存入数组返回即可。

/**
 * 堆        O(nlogk)   O(k)
 * @return : int[]
 * @param arr : 输入数组
 * @param k : 数值k
 * @author AoCan
 * @date 2021/8/11 16:27
 */
public static int[] getLeastNumbers2(int[] arr, int k){
    int[] vec = new int[k];
    // 排除 0 的情况
    if (k == 0) {
        return vec;
    }
    //num1是待插元素，num2是最后一个非叶子节点，当compare()返回的值<0时入队，>0时不入队
    PriorityQueue<Integer> queue = new PriorityQueue<>((num1, num2) -> num2 - num1);
    for (int i = 0; i < k; ++i) {
        queue.offer(arr[i]);
    }
    //第k+1个数开始入队
    for (int i = k; i < arr.length; ++i) {
        //如果遍历到的元素小于堆顶元素则将堆顶的元素弹出，并插入遍历到的元素
        if (queue.peek() > arr[i]) {
            queue.poll();
            queue.offer(arr[i]);
        }
    }
    //将大根堆的元素存入数组
    for (int i = 0; i < k; ++i) {
        vec[i] = queue.poll();
    }
    return vec;
}

PriorityQueue优先级队列

用法：

PriorityQueue<Integer> queue = new PriorityQueue<Integer>(new Comparator<Integer>(){
 @Override
 public int compare(Integer num1, Integer num2){  
 	return num2 - num1; 	  // 最大优先队列，return num2.compareTo(num1);
                          	  // 最小优先队列，return num1.compareTo(num2);
 }
});

//lambda表达式
PriorityQueue<Integer> queue = new PriorityQueue<>((num1, num2) -> num2 - num1);

Compare含义：

// num1是待插元素，num2是最后一个非叶子节点
compare(Integer num1, Integer num2)

具体场景

TopK 问题：

• 数组中最大的 K 个
  构造小根堆，堆顶为最小数，不断入队，当队列数大于 K 时，将最小的堆顶弹出，最后剩下的就是 K 个最大数

• 数组中最小的 K 个
  构造最大堆，堆顶为最大数，不断入队，当队列数小于 K 时，将最大的堆顶弹出，最后剩下的就是 K 个最小数

该题就是第二种

参考

1. 百度百科
2. 图解大根堆的堆排序
3. 如何构建一个大根堆
4. 堆排序
5. 数据结构—堆、大根堆、小根堆
6. PriorityQueue优先级队列用法